Simplify
不难想到其实题意就是让你求:
Solution
首先考虑暴力,我的话是枚举 \(l,r(l\in[1,n],l\in[1,r])\),然后 \(m\) 个单调队列先把 \(l\) 到 \(r\) 的 b 数组存进去,然后从 \(1\) 到 \(r\) 依次将超出范围的队头弹出维护最大值,\(\sum_{i=l}^ra_i\) 就直接前缀和。
时间复杂度为 \(O(n^2m)\),显然会炸,于是考虑优化。
枚举过程中保持单调不变的是 \(r\),而 \(l\) 会重复遍历……有重复的部分?
那么我们可以每次入完队后存一下这次的历史版本,以便在 \(r+1\) 的时候可以免去“\(m\) 个单调队列先把 \(l\) 到 \(r\) 的 b 数组存进去”这个操作。
但是任然解决不了问题。
想要将复杂度降下来,我们是不是可以考虑优化掉那个 \(O(n)\) 的枚举 \(l\),想想怎么才能把它优化掉……
简单,就是把每个 \(1\le j\le m\) 的 \(\max_{l\le i\le r}\{b_{i,j}\}\) 预处理出来,这样复杂度就降为 \(O(n^2+nm)\),但是,怎么预处理呢?
再思考思考,我们会发现一些性质(废话),就是在枚举 \(l\) 时单调队列的队头的 \(b\) 值是成单调递减的,且第 \(k\) 个队头 \(l_k\) 是会从 \(l_{k-1} + 1\) 保持到 \(l_k\) 的,再通俗一点,在 \(l\) 的遍历过程中,会有一段的最大值是不变的,再再再通俗一点,就是再一段区间里的最大值相等。
诶?差分!我们在 \(l_k\) 和 \(l_{k-1}\) 上进行差分,大概长这个样子:
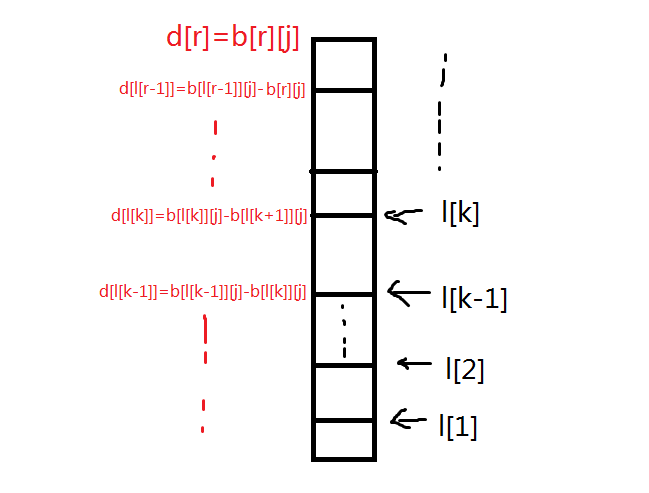
这样就好做多了,但是一个新的 \(r\) 入队时有可能会让这张图顶上的即队尾的几个 \(l\) 弹出,那我们用丹钓战维护啊(况且这图也像个丹钓战),在弹出过程中更改一下当前队尾的差分数组(减去 \(b_{l_k,j}-b_{l_{k+1},j}\)(本来是设为 \(0\),但是维护的是整个 \(m\) 行的差分,所以不能设为 \(0\))),出队出完了之后了的队尾要加上 \(b_{l_{p+1},j}-b_{r,j}\)(不是变为 \(b_{l_p,j}-b_{r,j}\) 的原因与上面的同理)。单调队列什么的丢掉。
我们需要预处理的 \(\max_{l\le i\le r}\{b_{i,j}\}\) 即为这个差分数组的前缀和。
这不就做完了吗。
顺便最优解。
Code
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 5005, M = 205;
inline char nc(){ static char buf[1000000],*p=buf,*q=buf; return p==q&&(q=(p=buf)+fread(buf,1,1000000,stdin),p==q)?EOF:*p++; } inline int read(){ int res = 0; char c = nc(); while(c<'0'||c>'9')c=nc(); while(c<='9'&&c>='0')res=res*10+c-'0',c=nc(); return res; }
int n, m;
int b[N][M], q[N][M], top[M];
ll d[N], sum[N], ans, a[N];//不开 long long 见祖宗
int main(){
n = read(); m = read();
for (int i = 2; i <= n; ++ i ) a[i] = read(), a[i] += a[i - 1];
for (int i = 1; i <= n; ++ i )
for (int j = 1; j <= m; ++ j )
b[i][j] = read();
for (int r = 1; r <= n; ++ r ) {
for (int j = 1; j <= m; ++ j ) {
int last = 0; //last 就是b[l[k+1]][j]
while(top[j] && b[q[top[j]][j]][j] < b[r][j]) {
// if(r == 2)cout << d[q[top[j]][j]] << endl;
d[q[top[j]][j]] -= 1ll * (b[q[top[j]][j]][j] - last);
last = b[q[top[j] -- ][j]][j];
}
d[q[top[j]][j]] -= 1ll * (b[r][j] - last);
q[ ++ top[j]][j] = r;
d[q[top[j]][j]] += 1ll * b[r][j];
//刚刚的差分
}
for (int l = r; l >= 1; -- l ) {
sum[l] = sum[l + 1] + d[l];
// cout << l << " " << r << "->" << d[l] << endl;
ans = max(ans, sum[l] - a[r] + a[l]);
}
}
printf("%lld", ans);
// fwrite(obuf,p3-obuf,1,stdout);
return 0;
}