Cordic算法

CORDIC 算法是坐标旋转数字计算的缩写，它最初用于三角函数的坐标变换，经过一定的推广后也可用于计算线形函数和双曲线函数(开平方根)。CORDIC算法只由移位操作和加减操作，因此，非常适合于在硬件使用。

Cordic算法
- 一、圆周系统
  - 1.1 旋转模式
    - 1.1.1 原理
  - 1.2 向量模式
    - 1.2.1 原理
    - 1.2.2 应用
- 二、双曲系统
  - 2.1 旋转模式
    - 2.1.1 原理
    - 2.1.2 应用
  - 2.2 向量模式
    - 2.2.1 原理
    - 2.2.2 应用

一、圆周系统

圆周系统下有两种模式，旋转模式和向量模式

1.1 旋转模式

1.1.1 原理

图1.1是一个单位圆。对于P/Q两点坐标为式（1.1）（1.2）

图1.1 旋转模式

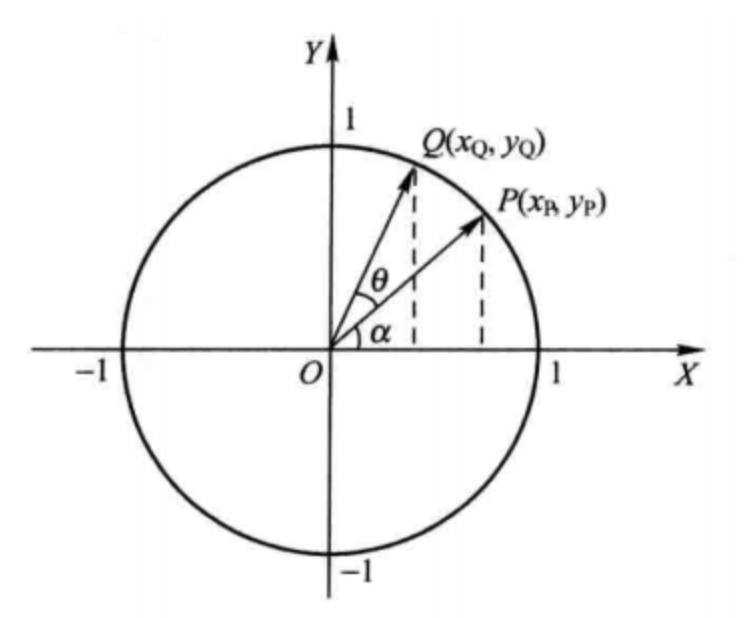
$$
\begin{cases}
x_P=cos\alpha\
y_P=sin\alpha\
\end{cases}
\tag{1.1}
$$

$$
\begin{cases}
x_Q=cos(\alpha+\theta)=cos\alpha cos\theta-sin\alpha sin\theta\
y_Q=sin(\alpha+\theta)=sin\alpha cos\theta+sin\theta cos\alpha\
\end{cases}
\tag{1.2}
$$

对于式（1.2），提出cosθ，并带入式（1.1）得到式（1.3）
$$
\begin{cases}
x_Q=cos\theta(x_P-y_Ptan\theta) \
y_Q=cos\theta(y_P+x_Ptan\theta) \
\end{cases}
\tag{1.3}
$$
由伪旋转图1.2可知，OP逆时针旋转θ°之后，理应到达OQ位置，根据三角函数关系，可得OQ的长度（模）刚好是OR的cosθ倍,相位一致**。因此R的坐标如式（1.4）。我们称OR是伪旋转，并先计算伪旋转，再补偿模值。

图1.2 伪旋转

$$ \begin{cases} x_R=x_P-y_Ptan\theta \\ y_R=y_P+x_Ptan\theta \\ \end{cases} \tag{1.4} $$

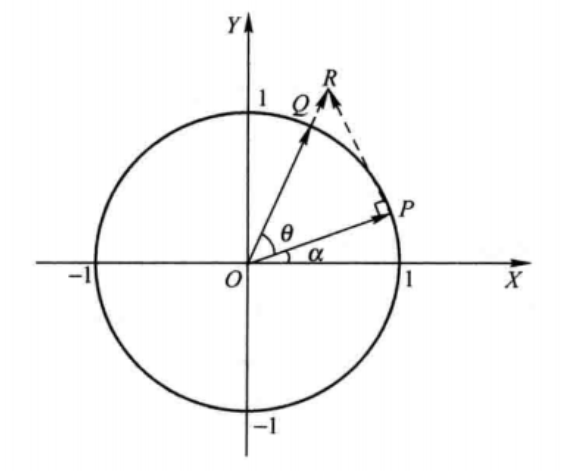
对于伪旋转的运算是算法的核心所在，首先分解成一次次的旋转迭代，先将θ分解如式（1.5）
$$
\theta=\sum_{i=0}^\infty\theta_i
\tag{1.5}
$$
然后把坐标计算分解，第i+1次的计算公式（1.6）
$$
\begin{cases}
x_{i+1}=x_i-y_itan\theta_i \
y_{i+1}=y_i+x_itan\theta_i \
\end{cases}
\tag{1.6}
$$
由于tanθ并不是一个容易得到的值，因此把tanθ替换，如式（1.7）.这里又引入了一个z，是干什么用的呢？要理解z，首先理解旋转迭代的过程，因为旋转迭代是可以看成围绕最终目标（这里是OQ）的来回振荡，如果这次转到目标上方（也就是相位超出目标），下次就要往下转（顺时针），反之同理。因此需要记录本次旋转后与目标的距离和相位情况，而这就是z的作用。而d决定旋转方向，如果zi是负数，说明相位落后，要增加相位，因此取负然后负负得正，使zi+1变大，相反，如果zi是正数，说明相位超前，需要相位回来一点，因此取负让zi+1等于zi减去本次微旋转角度θi。
$$
\begin{gather}
tan\theta_i=d_i2^{-i}
\tag{1.7}\
z_{i+1}=z_i-\theta_i=z_i-tan^{-1}(d_i2)
\tag{1.8}\
d_i=
\begin{cases}
+1&z_i\ge0 \
-1&z_i< 0 \
\end{cases}
\tag{1.9}\
\end{gather}
$$
伪旋转迭代完成后，需要进行补偿（也可以在旋转开始前补偿）。令补偿因子为K，则实际旋转迭代方程如（1.10）,由于x、y的次数相同，因此可以把补偿因子提出，结合式（1.7）累乘得到式（1.11）和式（1.12）。
$$
\begin{cases}
x_{i+1}=K_i(x_i-y_id_i2^{-i}) \
y_{i+1}=K_i(y_i+x_id_i2^{-i}) \
\end{cases}
\tag{1.10}
$$

$$
\begin{gather}
K_i=cos\theta_i=\frac{1}{\sqrt{1^2+{(2{-i}})^2}}
\tag{1.11}\
K=\prod_0^\infty K_i
\tag{1.12}\
\end{gather}
$$
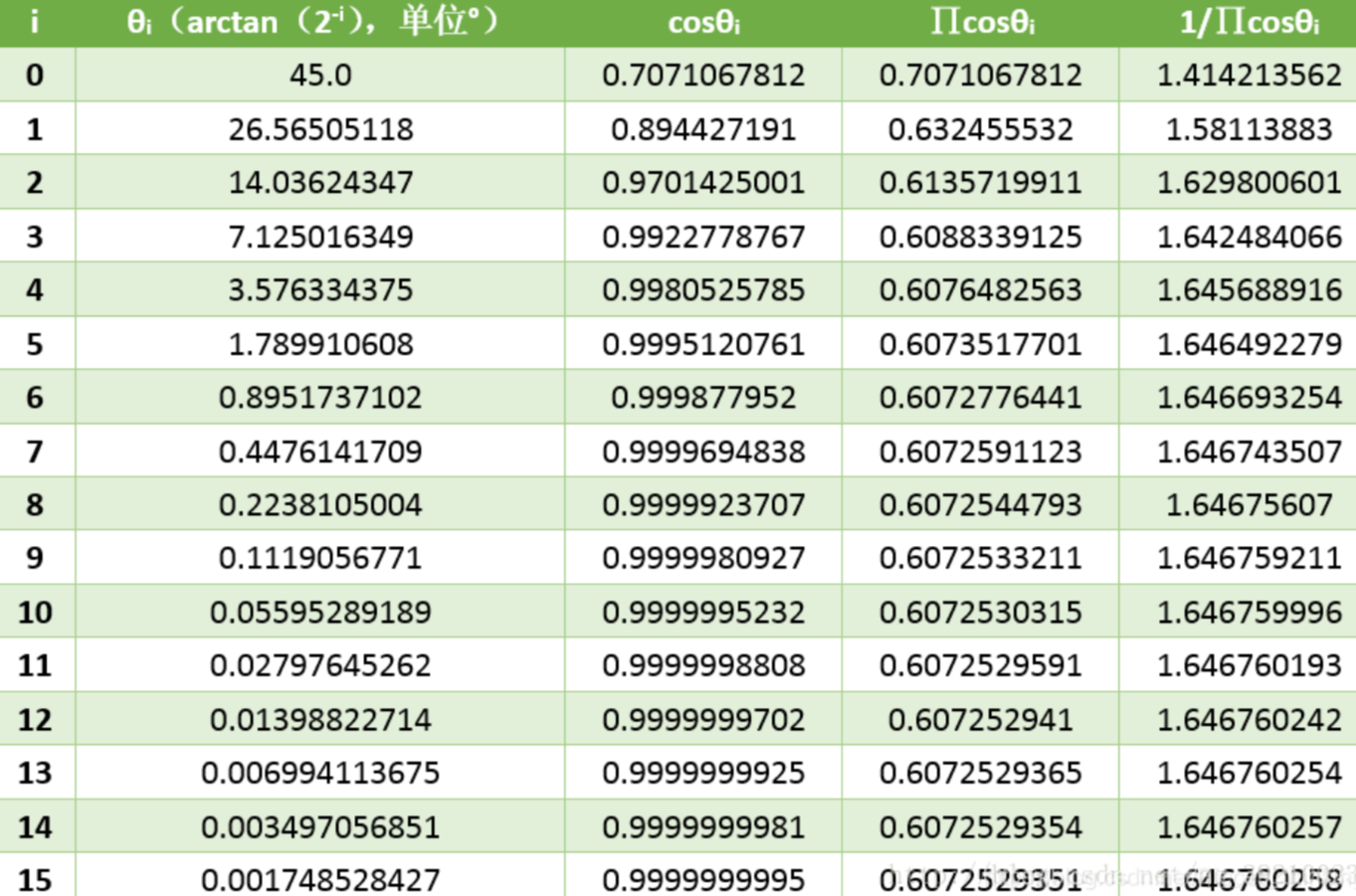
由于cosθi的值是固定的，如图1.3，因此可以提前把K算出来，取0.607252935.

图1.3 K取值表

记输入为x0、y0、z0,分别对应图1.1的xp、yp、角度θ**注意，这里的xn、yn是伪旋转输出结果，因此尚未模值补偿，因此等式（1.13）右边的真实坐标需要乘K的倒数**。经过n次迭代，最终结果可以表示为 $$ \begin{gather} \begin{cases} x_n=\frac{1}{K}(x_0cosz_0-y_0sinz_0) \\ y_n=\frac{1}{K}(y_0cosz_0+x_0sinz_0) \\ z_n=0 \end{cases} \tag{1.13} \end{gather} $$ #### 1.1.2 应用

旋转模式可以计算三角函数sin和cos，可以让z0为待求角度θ，y0为0，x0为K，输出为
$$
\begin{gather}
\begin{cases}
x_n=cos\theta \
y_n=sin\theta \
z_n=0
\end{cases}
\tag{1.14}
\end{gather}
$$

1.2 向量模式

1.2.1 原理

向量模式与旋转模式基本原理相似，都是在单位圆做旋转。区别在于向量模式求得是模长和角度，本质是直角坐标向极坐标的转换。图1.4即为向量模式，只有一个点P，经过n次迭代，最终使OP顺时针旋转到x轴正半轴上，从而得到角度。

图1.4 向量模式

伪旋转公式（1.15），由于目标是趋向x正半轴，因此决定旋转方向d的是y坐标，当y为正数，说明高于x轴，需要顺时针移动，则d为负，反之同理。 $$ \begin{cases} x_{i+1}=x_i-y_id_i2^{-i} \\ y_{i+1}=y_i+x_id_i2^{-i} \\ z_{i+1}=z_i-\theta_i=z_i-tan^{-1}(d_i2^{-i})\\ d_i= \begin{cases} -1&y_i\ge0 \\ +1&y_i< 0 \\ \end{cases} \end{cases} \tag{1.15} $$ 同样，记输入为x0、y0、z0,分别对应图1.4的xp、yp、角度θ.伪旋转的最终结果为式（1.16），xn对应最终模值，yn对应差值，zn对应旋转角度。这里有个小思考，为什么zn是加θ呢？我的想法是，观察式1.15可知，第一次计算z1的值时，d0为负，因此实际z0是加上θ0（45°）。以此类推，每当高于x轴时（y>0），z是增加的，而OP又是从高于x轴的位置顺时针旋转，因此z最终结果必定是正。 $$ \begin{gather} \begin{cases} x_n=\frac{1}{K}\sqrt{x_0^2+y_0^2} \\ y_n=0 \\ z_n=z_0+\theta=z_0+tan^{-1}(y_0/x_0) \end{cases} \tag{1.16} \end{gather} $$

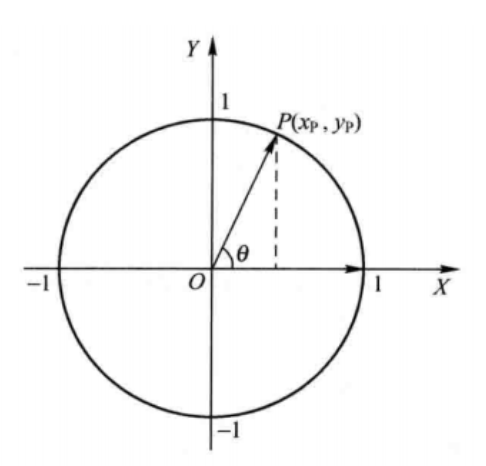
1.2.2 应用

求复数的模和相位

令x0，y0为分别为复数x+yi的实部和虚部，并且对xn输出模值校正（乘K），结果x'n输出模值，z0输出相位。实际操作时也可把x0和y0先校正。

求反正切

令x=1，y0为角度，则z0输出y0的反正切值。由于不涉及幅度，因此不需要校正。

CORDIC算法详解(一)-CORDIC 算法之圆周系统之旋转模式_cordic碎碎思-CSDN博客

CORDIC算法详解(二)-CORDIC 算法之圆周系统之向量模式_cordic向量模式-CSDN博客

二、双曲系统

2.1 旋转模式

2.1.1 原理

在双曲系统，点的坐标落在双曲线正半轴上，分析方法与圆周系统一样，只不过方程和坐标略有不同。

图2.1 双曲系统

由图得出PQ两点坐标，注意别跟正弦余弦函数搞混 $$ \begin{cases} x_P=cosh\alpha\\ y_P=sinh\alpha\\ \end{cases} \tag{2.1} $$

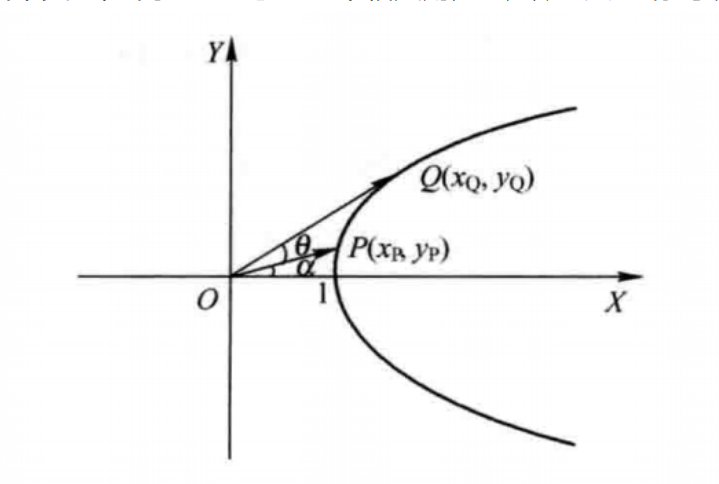
$$
\begin{cases}
x_Q=cosh(\alpha+\theta)=cosh\alpha cosh\theta+sinh\alpha sinh\theta\
y_Q=sinh(\alpha+\theta)=sinh\alpha cosh\theta+sinh\theta cosh\alpha\
\end{cases}
\tag{2.2}
$$

将式（2.1）带入式（2.2），并提出coshθ，得到式（2.3)
$$
\begin{cases}
x_Q=cosh\theta(x_P+y_Ptanh\theta) \
y_Q=cosh\theta(y_P+x_Ptanh\theta) \
\end{cases}
\tag{2.3}
$$
然后就是熟悉的伪旋转分解：
$$
\begin{cases}
x_{i+1}=x_i+y_id_i2^{-i} \
y_{i+1}=y_i+x_id_i2^{-i} \
z_{i+1}=z_i-\theta_i=z_i-tanh^{-1}(d_i2)\
d_i=
\begin{cases}
+1&z_i\ge0 \
-1&z_i< 0 \
\end{cases}
\end{cases}
\tag{2.4}
$$
当然，由于是cosh而不是cos，因此迭代过程略有不同。首先因为分母不可以为零，因此跳过第一次迭代，当迭代到4、13、40等满足i=3k+1形式，必须重复迭代一次，即1,2,3,4,4,5... 另外模补偿因子也有不同，见式（2.5），K≈1.20749706
$$
\begin{gather}
K_i=cosh\theta_i=\frac{1}{\sqrt{1^2-{(2{-i}})^2}}\
K=\prod_1^\infty K_i
\end{gather}
\tag{2.5}\
$$
由于i=0取不到，因此从1开始迭代，最终迭代结果如式（2.6）
$$
\begin{gather}
\begin{cases}
x_n=\frac{1}{K}(x_1coshz_1-y_1sinhz_1) \
y_n=\frac{1}{K}(y_1coshz_1+x_1sinhz_1) \
z_n=0
\end{cases}
\end{gather}
\tag{2.6}
$$

2.1.2 应用

旋转模式下可以求双曲余弦函数和双曲正弦函数，令x1=1/K,y1=0,z1=θ,得到
$$
\begin{gather}
\begin{cases}
x_n=cosh\theta\
y_n=sinh\theta\
z_n=0
\end{cases}
\tag{2.7}
\end{gather}
$$

2.2 向量模式

2.2.1 原理

在双曲系统，点的坐标落在双曲线正半轴上，分析方法与圆周系统一样，只不过方程和坐标略有不同，跳过第一次迭代。迭代分析过程表达式（2.8）
$$
\begin{cases}
x_{i+1}=x_i+y_id_i2^{-i} \
y_{i+1}=y_i+x_id_i2^{-i} \
z_{i+1}=z_i-\theta_i=z_i-tanh^{-1}(d_i2)\
d_i=
\begin{cases}
+1&y_i\lt0 \
-1&y_i\ge0 \
\end{cases}
\end{cases}
\tag{2.8}
$$
直接给出结果式（2.9）
$$
\begin{gather}
\begin{cases}
x_n=\frac{1}{K}\sqrt{x_1^2-y_12} \
y_n=0 \
z_n=z_1+tanh^{-1}(y_1/x_1)
\end{cases}
\tag{2.9}
\end{gather}
$$

2.2.2 应用

可以求开方和对数，令x1=θ+1，y1=θ-1，z1=0
$$
\begin{gather}
\begin{cases}
x_n=\frac{2}{K}\sqrt{\theta} \
y_n=0 \
z_n=z_1+tanh^{-1}(\frac{\theta-1}{\theta+1})=\frac{1}{2}\ln\theta
\end{cases}
\tag{2.10}
\end{gather}
$$