
注意:博主并不会最小左转法!
什么是平面图:
如果能将一张图放到平面上并且边不相交,那么这张图就被称为平面图,比较常见的平面图就是网格图。
像这张图就是平面图:
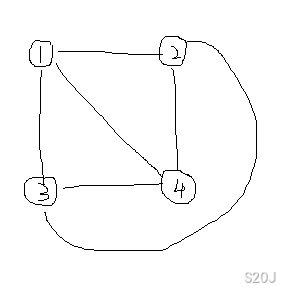
但是这张图就不是平面图:

这条红边放到外面也会和 \((1,4)\) 这条边相交。
关于平面图的一些概念:
-
有限面:一张平面图将一个平面分成了很多个部分,面积是有限的部分被称为有限面。
-
无限面:同上,面积无限的部分被称为无限面。
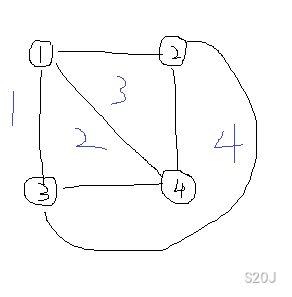
比如这张图,面 \(2,3,4\) 都是有限面,而面 \(1\) 是无限面。
- 欧拉公式:\(\text{点数}-\text{边数}+\text{面数}=2\)。
- 常用性质:对于 \(n \ge 3\) 的联通简单平面图,有 \(m \le 3\cdot n-6\),其中 \(n\) 是点数,\(m\) 是边数。
什么是对偶图:
有源汇:将源点和汇点用另一条边链接,将每个面看成点,两个相邻的面连边,边权是邻边的权值。
比如这张图:(设源点为 \(1\),汇点为 \(5\))
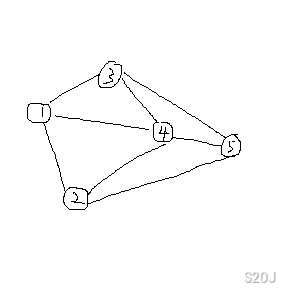
它的对偶图就是:
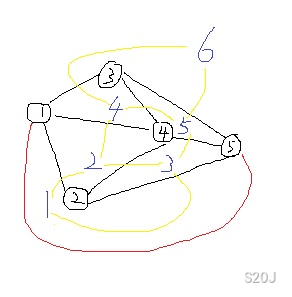
新图中源点为 \(1\),汇点为 \(6\)。(因为这里多加了一条红边,所以有可能加不了,然后就寄了,但是一般题目都是用网格图,所以没啥事)
对偶图有非常神奇的性质:将每一条从源点到汇点的路径对应着一个割,至于为什么,大概就是你将经过的边全部割掉,对偶图上 \(S\) 和 \(T\) 就连通了,说明除了我加的红边之外没有路径能从平面图上的 \(S\) 到 \(T\) 了。
根据这个性质我们就能优化一些东西。
无源汇:只要不加上面那张图的红边就好了,割就是一个经过无限面的环。
若图为有向图,不难发现原图上的边权对应的是逆时针旋转 \(90^{\circ}\) 的边权,比如上面那张图,平面图上边 \((1,3)\) 对应的就是对偶图上的 \((4,6)\),而 \((3,1)\) 则是 \((6,4)\)。
例题:
洛谷 P4001 [ICPC-Beijing 2006] 狼抓兔子
这玩意就是一个最小割,但是直接流复杂度是 \(O(n^6)\) 的虽然能过,我谔谔。
首先这个图显然是平面图,题目又是让求最小割,考虑转成对偶图,对偶图上从起点到终点每一条路径都是一个割,所以最小割就是最短路,然后跑最短路就没了。(
洛谷 P3209 [HNOI2010] 平面图判定
首先发现边有那么多根本没用,\(m\) 大于 \(3\cdot n-6\) 的直接输出 \(NO\) 就好了。
将一条边拆成两个点,一个为这条边放到环内部,一个为这条边放到环外部,枚举两条边 \(i,j\) ,若他们能放到同一侧就不连边,否则就将 \(i\) 的放在环内部点和 \(j\) 的放在环外部点连起来,将 \(i\) 的放在环外部点和 \(j\) 的放在环内部点连起来,因为边是无向边,所以直接并查集就好了,不用 \(\text{2-sat}\)(这个处理的是有向图)。
这样时间复杂度就是 \(O(Tn^2)\) 的,可以通过,注意判相交的细节。
洛谷 P2046 [NOI2010] 海拔
发现我走太高并不优,这样只会徒加贡献,所以每个点高度只可能是 \(0,1\),思考一下发现高度为 \(0\) 的和高度为 \(1\) 的一定是一个连通块,因为你考虑一个点周围高度全是 \(1\),只有他是 \(0\),不如直接把他高度也变成 \(1\),这样一定不劣。
现在题目就被转化的很简单了,现在就等于给每个点求一个高度,使得对于每一条从起点到终点的路径高度变化且只变化一次,也就是我们将所有左右高度不一样的边割掉,起点终点不连通,现在我们就转化成了最小割了,建对偶图直接跑就行了。
洛谷 P7916 [CSP-S 2021] 交通规划
首先先思考一下 \(k=2\) 怎么做,不难发现这个跟上面那个海拔是一毛一样的,就是将白点看成高度为 \(0\),黑点看成高度为 \(1\)。
考虑怎么推广这个东西,首先有一个很暴力的直接优化,就是直接在原图上跑最小割,拼上上面的 \(k=2\),这样就可以得到 \(80pts\) 了。
其实还有一个 \(k=3\),这个也挺有用的。(但是部分分没给)
因为流没有前途,所以还是从对偶图角度考虑。
不难发现一定有两个颜色相同,并且他俩一定相邻,就比如说下图:
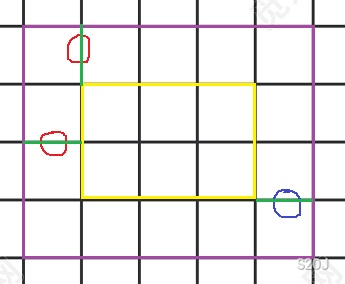
假设原图是黄框,我们把黑色附加点看成红色点,白色附加点看成蓝色点,现在我们把网格图向外扩充一圈,现在将图标号,最外层的编号是按绿线分割的,编号完也就是下图:(其实上面的文字解释我自己都看不懂)
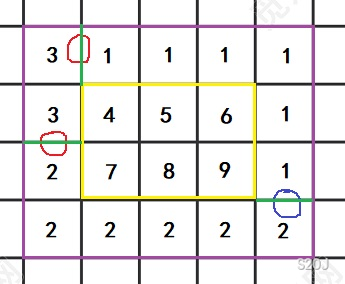
考虑怎么将红蓝点断开,不难发现就是让 \(1,2\) 成为对偶图源汇点。
同理,如果有很多红点很多蓝点,但是所有红点都相邻,也可以让”左边和红点相邻,右边和蓝点相邻“的面作为源点,让”左边和蓝点相邻,右边和红点相邻“(这里的左右都是按照射线编号顺序编号的左右,例如上图中的 \(2\) 为到达面,这个不是肉眼看的左右)的面作为汇点直接跑最短路。
正解:
现在你什么性质都没有了?,但是不难从上面的得出,我要是相同颜色的点相邻是没有任何用的(同 \(k=3\),所以下面不考虑这种情况),我们定义”左边和红点相邻,右边和蓝点相邻“的面为出发面,”左边和蓝点相邻,右边和红点相邻“的面为到达面,首先这两种面的数量肯定一样,考虑我们给他们配对,还是按题目中给的射线编号顺序方法给所有出发面到达面重标号,假设我们将编号为 \(l\) 的面和编号为 \(r\) 的面匹配(这里要求两个面不是同一种面),不妨假设 \(l\) 为出发面,我们直接跑从 \(l\) 到 \(r\) 的最短路,然后把所有最短路上的边割掉,发现这个操作使得 \(l,r\) 内所有的蓝点都到达不了这个 \(l\) 左边相邻的红点了,就比如下图:
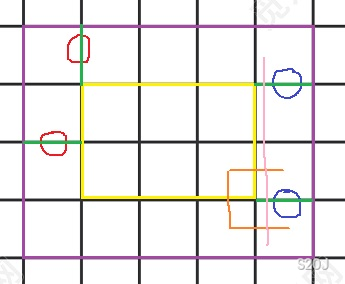
你的 \(l\) 是右上角的红点到右上角的蓝点,\(r\) 是左下角的蓝点到右边的另一个红点,你这样建图不会像橙边这样割,因为上面那个蓝点还是能到达右上角的红点,但是可以像粉边这样割,然后你发现你这样分出来的一定是正确的,因为你考虑一个 \(1,4\),\(2,3\) 的配对方法(下图),你在中间留的是一样颜色的点,割出去的是颜色一样的点,归纳一下就行了。
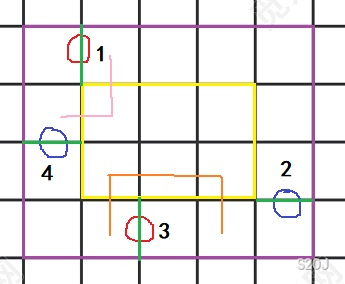
那么为什么这样配对找到的最小值一定是答案呢?
额,你发现这玩意好像就是和答案一一对应的。(最终答案中肯定没有卐的形状,怎么着都能断一些边)
然后发现你的配对方案和括号序列很像,不会相交(即出现 \(1,3\) 配对,\(2,4\) 配对这种情况),因为如果这样的话你 \(1,3\) 的最短路一定和 \(2,4\) 的最短路相交,相交是不优的,不如改成 \(1,2\) 配对,\(3,4\) 配对。
把这个段环成链,随便 \(dp\) 一下就好了。
设 \(f_{l,r}\) 表示将 \([l,r]\) 匹配好的最小代价,转移有:
\(f_{l,r}=\min\{f_{l+1,r-1}+dis_{l,r},\min\limits_{k=l}^{r}\{f_{l,k}+f_{k+1,r}\}\}\).