二、证明等式(3.16):a ^ {\log_b c} = c ^ {\log_b a}。
文心一言:

chatgpt:
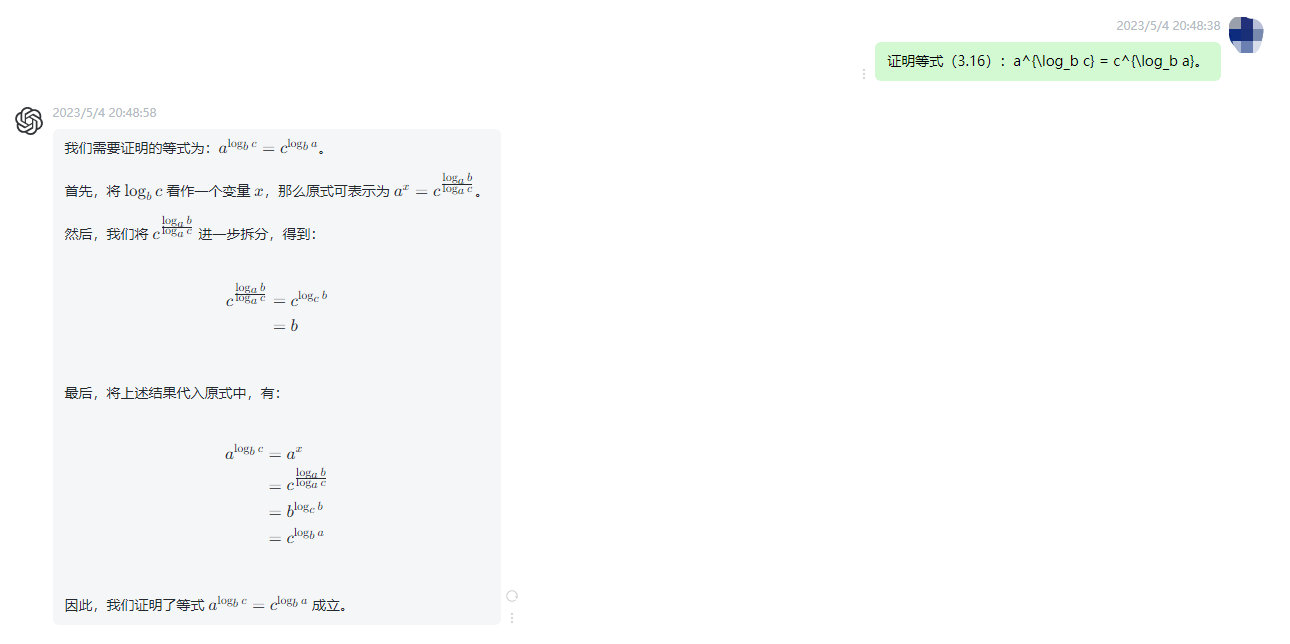
我们需要证明的等式为:$a^{\log_b c} = c^{\log_b a}$。
首先,将 $\log_b c$ 看作一个变量 $x$,那么原式可表示为 $a^x = c^{\frac{\log_a b}{\log_a c}}$。
然后,我们将 $c^{\frac{\log_a b}{\log_a c}}$ 进一步拆分,得到:
$$
\begin{aligned}
c^{\frac{\log_a b}{\log_a c}} &= c^{\log_c b} \
&= b
\end{aligned}
$$
最后,将上述结果代入原式中,有:
$$
\begin{aligned}
a^{\log_b c} &= a^x \
&= c^{\frac{\log_a b}{\log_a c}} \
&= b^{\log_c b} \
&= c^{\log_b a}
\end{aligned}
$$
因此,我们证明了等式 $a^{\log_b c} = c^{\log_b a}$ 成立。
三、证明等式(3.19):\lg(n!) = \Theta(n \lg n)。并证明 n! = \omega(2 ^ n) 且 n! = o(n^n)。
文心一言:

chatgpt:
首先,我们证明等式 $\lg(n!) = \Theta(n \lg n)$。
由斯特林公式(Stirling's formula),可得:
$$
\ln n! = n \ln n - n + \mathcal{O}(\ln n)
$$
两边同时取以 2 为底的对数,则有:
$$
\begin{aligned}
\log_2 n! &= \frac{\ln n!}{\ln 2} \
&= \frac{n \ln n - n + \mathcal{O}(\ln n)}{\ln 2} \
&= n \frac{\ln n}{\ln 2} - \frac{n}{\ln 2} + \mathcal{O}\left(\frac{\ln n}{\ln 2}\right)
\end{aligned}
$$
因为 $\frac{\ln n}{\ln 2}$ 等于 $\Theta(\log n)$,所以可得:
$$
\log_2 n! = \Theta(n \log n)
$$
因此,$\lg(n!) = \Theta(n \lg n)$ 得证。
接下来,我们证明 $n! = \omega(2^n)$。根据定义,需要证明:
$$
\lim_{n\to\infty} \frac{n!}{2^n} = \infty
$$
考虑到:
$$
\begin{aligned}
\frac{(n + 1)!}{n!} &= n + 1 \
&> 2
\end{aligned}
$$
因此,$n!$ 至少每乘以 2 次就要增长一倍,即:
$$
\begin{aligned}
n! &= 1 \times 2 \times 3 \times \cdots \times n \
&> 2 \times 2 \times 2 \times \cdots \times 2 \
&= 2^n
\end{aligned}
$$
因此,$n! = \omega(2^n)$ 成立。
最后,我们证明 $n! = o(n^n)$。根据定义,需要证明:
$$
\lim_{n\to\infty} \frac{n!}{n^n} = 0
$$
将 $n!$ 展开,则有:
$$
\begin{aligned}
n! &= 1 \times 2 \times 3 \times \cdots \times n \
&< n \times n \times n \times \cdots \times n \
&= n^n
\end{aligned}
$$
因此,$\frac{n!}{n^n} < 1$,即 $\frac{n!}{n^n} \to 0$ 当 $n \to \infty$。因此,$n! = o(n^n)$ 成立。
综上所述,我们证明了等式 $\lg(n!) = \Theta(n \lg n)$,以及 $n! = \omega(2^n)$ 和 $n! = o(n^n)$。

