简述
整除分块这个东西听起来不是很抽象,但是我理解起来的确有点抽象(可能因为我太菜了吧)。那就先放张图:
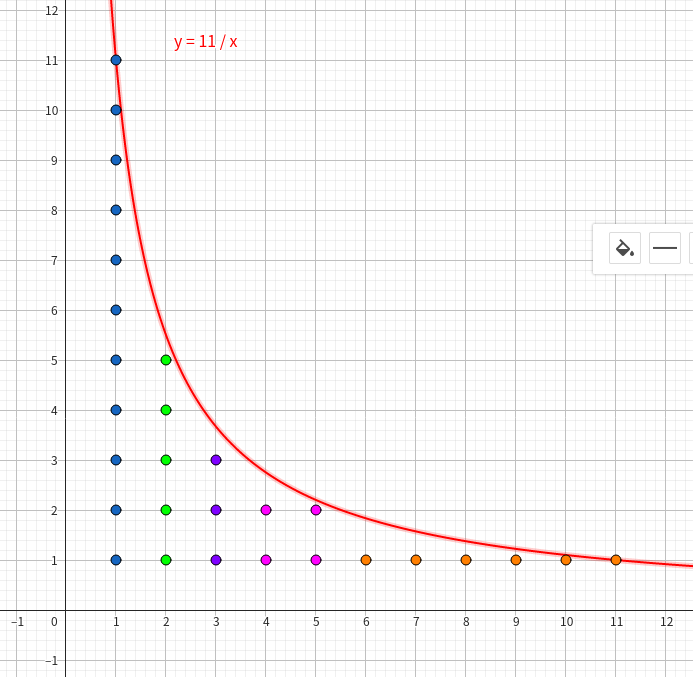
其实就是颜色相同的点被分成了一块。如果序列总长度是 \(n\),某一个区间左端点是 \(l\),那么 \(r = \lfloor \dfrac{n}{\lfloor \dfrac{n}{l} \rfloor} \rfloor\)。
所以整除分块主要是用来处理一些向下取整(或取模,因为取模也可以用向下取整的式子表示)的问题。
这个玩意的代码实现也挺模式化的,详见例题代码。
例题
UVA11526 H(n)
\(T\) 组数据,每组数据给定一个 \(n\),求 \(H(n) = \sum \limits _ {i = 1} ^ {n} \lfloor \dfrac{n}{i} \rfloor\)。
最基本的板子题,考虑整除分块,枚举到 \(l, r\),令 \(ans \leftarrow ans + (r - l + 1) \times \lfloor \dfrac{n}{i} \rfloor\)。
#include <bits/stdc++.h>
#define int long long
using namespace std;
int t, n, l, r, ans;
signed main() {
scanf("%lld", &t);
while (t--) {
scanf("%lld", &n);
l = 1; r = 0; ans = 0;
while (l <= n) {
r = n / (n / l);
ans += (r - l + 1) * (n / l);
l = r + 1;
}
printf("%lld\n", ans);
}
}
P1403 [AHOI2005] 约数研究
给定 \(n\),设 \(f_i\) 为 \(i\) 的约数个数,求 \(\sum\limits _ {i = 1} ^ n f_i\)。
方法一:显然这是个积性函数,直接按着题意跑一遍线性筛即可。
方法二:显然最大的约数是 \(n\),可以转化为从 \(1\) 到 \(n\),每一个数能作为多少个数的约数,同上面的例题。
P2261 [CQOI2007] 余数求和
给定 \(n, k\),求 \(\sum\limits _ {i = 1} ^ n k \bmod i\)。
将 \(k \bmod i\) 转化成 \(k - i \times \lfloor \dfrac{k}{i} \rfloor\),然后求的时候乘上一个等差数列通项公式,就会做了。
#include <bits/stdc++.h>
#define int long long
using namespace std;
int n, k, l(1), r, ans;
signed main() {
cin >> n >> k;
ans = n * k;
for (l = 1; l <= n; l = r + 1) {
if (k >= l) r = min(k / (k / l), n);
else r = n;
ans -= (l + r) * (r - l + 1) / 2 * (k / l);
}
cout << ans << '\n';
}
P3935 Calculating
若 \(x\) 分解质因数结果为 \(x=p_1^{k_1}p_2^{k_2}\cdots p_n^{k_n}\),令\(f_x=(k_1+1)(k_2+1)\cdots (k_n+1)\),求 \(\sum\limits_{i=l}^r f_i \bmod 998244353\)。
这个题面的结论很常见,\(f_x\) 就是 \(x\) 约数个数,看我另一篇博客的解释。
跟前两个例题一样,就不废话了。
P2260 [清华集训2012] 模积和
给定 \(n, m\),求 \((\sum\limits_{i=1}^{n} \sum\limits_{j=1}^{m} (n \bmod i) \times (m \bmod j), i \neq j)\) \(\bmod 19940417\) 的值。
这题一看就是先推式子,然后就是乱搞。别的都好说,有两个地方需要注意。
有一项是 \(\sum\limits _ {i = 1} ^ {n} i^2 \times \lfloor \dfrac{n}{i} \rfloor \times \lfloor \dfrac{m}{i} \rfloor\)。
对于 \(i^2\) 的有一个结论:
证明:
考虑构造。存在 \((n + 1) ^ 3 - n ^ 3 = 3 \times n ^ 2 + 3 \times n + 1\),从大到小递推再累加即可构造出来。
对于 \(\lfloor \dfrac{n}{i} \rfloor \times \lfloor \dfrac{m}{i} \rfloor\),就是假定先用 \(\lfloor \dfrac{n}{i} \rfloor\) 分好块,再用 \(\lfloor \dfrac{m}{i} \rfloor\) 把原有的块再分 \(m\) 个,代码实现就是 r = min(n / (n / i), m / (m / i))。时间复杂度只会影响常数级别。
一定要注意取模,还有写对符号!!我就是因为把取模打成乘号调了好长时间。
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int P(19940417);
int n, m, ans, inv2(9970209), inv6(3323403);
inline int read() {
int f(1), x(0);
char c = getchar();
for (; !isdigit(c); c = getchar()) if (c == '-') f = -1;
for (; isdigit(c); c = getchar()) x = (x << 1) + (x << 3) + (c & 15);
return f * x;
}
inline int Sum(int x) {
return x * (x + 1) % P * (2 * x + 1) % P * inv6 % P;
}
inline int Range1(int l, int r) {
return (l + r) * (r - l + 1) % P * inv2 % P;
}
inline int Range2(int l, int r) {
return (Sum(r) - Sum(l - 1) + P) % P;
}
void solve1() {
int res1 = n * n % P, res2 = m * m % P, res3 = n * n % P * m % P; // fu hao da cuo le
for (int l = 1, r; l <= n; l = r + 1) {
r = n / (n / l);
res1 = (res1 + P - Range1(l, r) * (n / l) % P) % P;
}
for (int l = 1, r; l <= m; l = r + 1) {
r = m / (m / l);
res2 = (res2 + P - Range1(l, r) * (m / l) % P) % P;
}
ans = res1 * res2 % P;
ans = (ans + P - res3) % P;
}
void solve2() {
int a(0), b(0), c(0);
for (int l = 1, r; l <= n; l = r + 1) {
r = min(n / (n / l), m / (m / l));
a = m * Range1(l, r) % P * (n / l) % P;
b = n * Range1(l, r) % P * (m / l) % P;
c = Range2(l, r) * (n / l) % P * (m / l) % P;
ans = (ans + a + b - c + P) % P;
}
}
signed main() {
n = read(); m = read();
if (n > m) swap(n, m);
solve1();
solve2();
printf("%lld\n", ans);
}
P3579 [POI2014] PAN-Solar Panels
给定区间 \([a, b], [c, d]\),求 \(\max\{\gcd(i, j)\}, i \in [a, b], j \in [c, d]\)。
这道题很好,并不是板子,需要一定思考。
为了方便,先设 \(b = \min(b, d)\)。
显然我们知道,答案在 \([1, b]\) 这个区间里。一个很暴力的思路就是直接把答案 \(i\) 从 \(1\) 枚举到 \(b\),显然会寄,那么就用整除分块优化,显然每次枚举到的是一段区间 \([l, r]\),也就是对于 \(\forall i \in [l, r], \dfrac{b}{i}\) 都相等。根据题意要选最大的,所以直接选 \(r\) 即可。
还有一个性质,就是若区间 \([l, r]\) 存在 \(x\) 的倍数,则 \(\lfloor \dfrac{l}{x}\rfloor < \lfloor \dfrac{r}{x} \rfloor\)。(这里的 \(l, r\) 不同于上面的 \(l, r\))
这样就可以在枚举 \(r\) 的同时判断 \(r\) 是否合法了。
#include <bits/stdc++.h>
using namespace std;
int n, a, b, c, d, ans;
int main() {
scanf("%d", &n);
while (n--) {
scanf("%d%d%d%d", &a, &b, &c, &d);
for (int l = 1, r; l <= min(b, d); l = r + 1) {
r = min(b / (b / i), d / (d / i));
if (b / i * i >= a && d / i * i >= c) ans = r;
}
printf("%d\n", ans);
}
}