T1

https://www.luogu.com.cn/problem/P2340

solution

01背包。
我们可以做出如下分析:

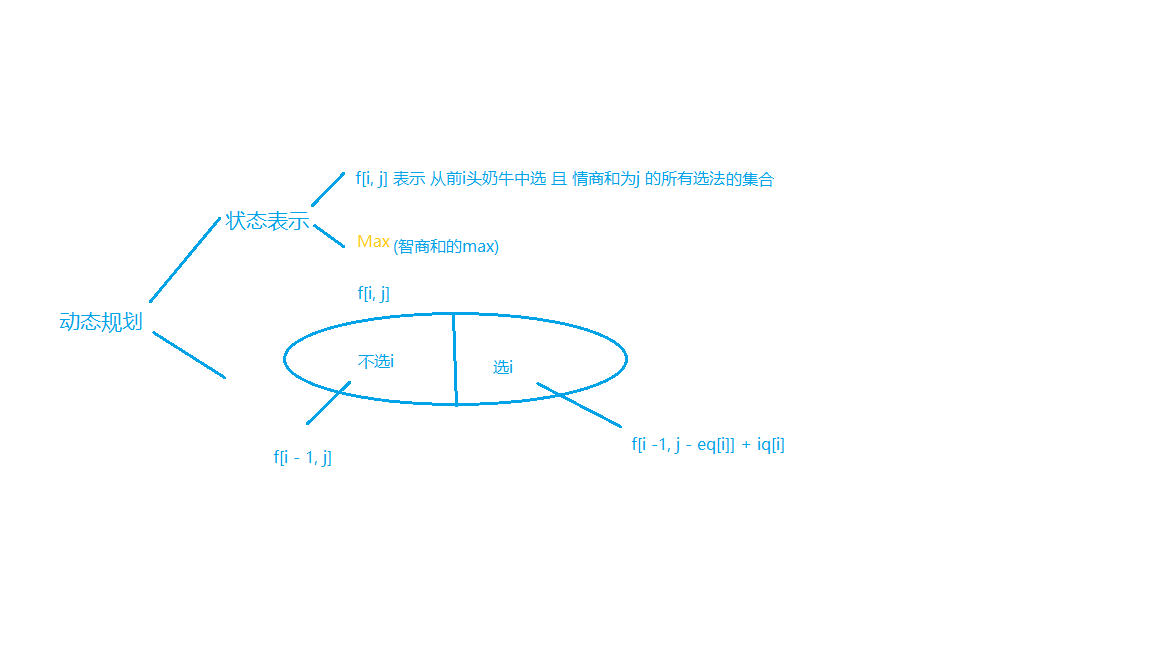
边界: $f[0][0] = 0$
最好初始化负无穷因为有负数比如$f[i - 1, j - eq[i]]$ 可能是负的我们拿0更新就会错误实际上不存在这个方案
目标: $max${$f[n, 0 ~ 取得最大数]$}$

就如此吗
我们可以发现空间是开不下的并且$f[i]$ 只与$f[i - 1]$因此我们可以使用滚动数组优化
也可以优化一维:
具体来说我们要保证用到的 $f[j - eq[i]]$ 的第一维是 $i - 1$
我们可以分类一下

对于$eq[i] >= 0$ 我们发现总是用$<j$的第二维因此我们要保证他还未被更新我们就可以倒着更新
对于$eq[i] < 0 $ 我们同理就可正着更新

那么还有一个问题我们第二维有可能是负的!!

没关系我们只需要加一个偏移量就可以

这个数一定要开大!!!(血的教训qwq 白掉80pts)

代码

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>

using namespace std;

const int N = 410, M = 400010;

int f[2][M << 1]; //开两倍
int n, m;
int iq[N], eq[N];
int res; 
int main()
{
	scanf("%d", &n);
	for (int i = 1; i <= n; i ++ )
	{
		scanf("%d%d", &iq[i], &eq[i]);
		
		m += max(iq[i], 0);
	}
	
	memset(f, -0x3f, sizeof f);
	f[0][M] = 0;
	for (int i = 1; i <= n; i ++ )
	{
		for (int j = 0; j <= m + M; j ++ )
		{
			f[i & 1][j] = f[(i - 1) & 1][j]; //不选i 
			f[i & 1][j] = max(f[i & 1][j], f[(i - 1) & 1][j - iq[i]] + eq[i]); //选i
		}
	} 
	
	//答案 从M(实际是0) 开始枚举
	for (int i = M; i <= m + M; i ++ )
	{
		if (f[n & 1][i] >= 0) res = max(res, f[n & 1][i] + i);
	}
	
	
	printf("%d\n", res - M); //别忘了减偏移量
	
	return 0;
}

T2

https://www.luogu.com.cn/problem/P1466

solution

01背包。

我们先来转化下题意：

给定$1$ ~ $n$ $n$个数从中选任意多个数使得选的数的和和不选的数的和相等
进一步因为最后两边和肯定是整个集合的和即给定$1$ ~ $n$ $n$个数从中选任意多个数使得选的数的和和不选的数的和相等并且和为$1$ ~ $n$ 的和($(1 + n)* n / 2$)
最后 给定$1$ ~ $n$ $n$个数从中选任意多个数每个数只能选1次使得选的数的和是 $(1 + n) * n / 4$
很熟悉吧？这不01背包嘛

令$m$ $=$ $(1 + n) * n / 4$
我们可以做出如下分析:

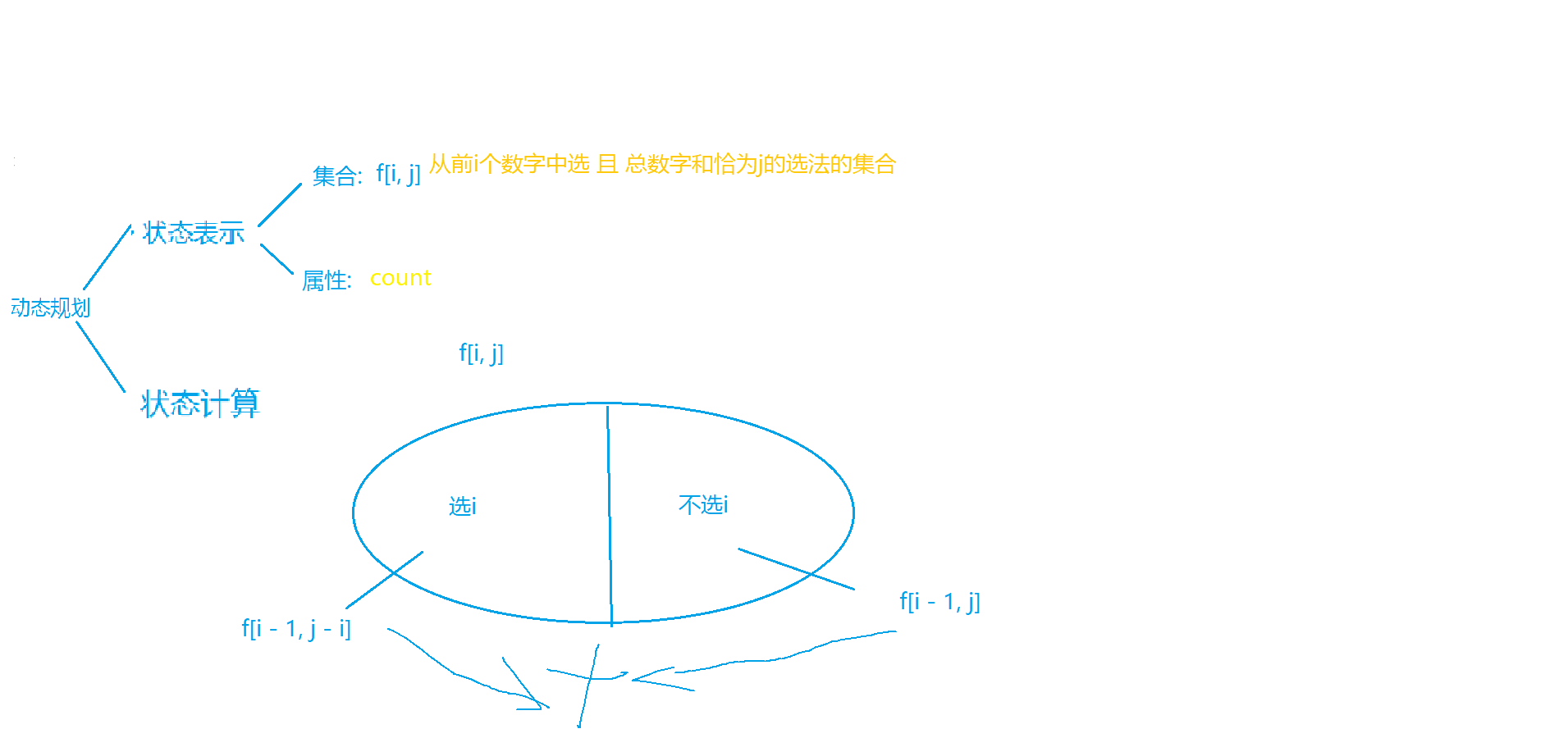
边界: $f[0][0] = 1$
目标: $f[n][m]$
优化一波一维倒着枚举就完了
特判如果 $(1 + n)* n / 2$是奇数直接不可能输出$0$

代码

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>

using namespace std;

typedef long long LL;

const int N = 45, M = (1 + N) * N >>1;

int n, m;
LL f[M];

int main()
{
	cin >> n;
	
	m = (1 + n) * n >> 2;
	if (((1 + n) * n >> 1) & 1)
	{
		puts("0");
		return 0;
	}
	f[0] = 1; 
	for (int i = 1; i <= n; i ++ )
		for (int j = m; j >= i; j -- )
			f[j] += f[j - i];
	
	cout << (f[m] >> 1) << endl; //答案两两一对 如果剩下一个不用管

	
	return 0;
}

T3

https://www.luogu.com.cn/problem/P2722

solution

完全背包板子。。。
种类看成物品时间看成体积总分看成价值

代码

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 10010;

int f[N];
int v, w;
int n, m;

int max(int a, int b)
{
	return a > b ? a : b;
}

int main()
{
	scanf("%d%d", &m, &n);
 	
 	for (int i = 0; i < n; i ++ )
 	{
 		scanf("%d%d", &w, &v);
 		for (int j = v; j <= m; j ++ )
 			f[j] = max(f[j], f[j - v] + w);
	}
	
	printf("%d\n", f[m]);
	
	return 0; 
}

T4

https://www.luogu.com.cn/problem/P5662

solution

本场mvp性质：

在某一种方案中，如果我们在第$i$天买入第$j$天卖出，其中 $i<j$，则等价于在第 $i$ 天买入，第 $i+1$ 天卖出，第 $i+1 $天再买入, …, 在第 $j$ 天卖出。

我们的交易总是前一天买入后一天卖出。
于是我们贪心：
对于每一天尽可能使下一天钱最多。
也好证明：

假设我们不让下一天钱最多 而取得最优解的话
那我们可以把这步替换成 让下一天钱最多 的方案（都可以买嘛） 而答案不会变劣 可能更优 
由决策包容性 证毕

此时就是完全背包问题了。

把股票看成物品
把 上一天留下来的钱 看成 背包容量
把 今天买入花的钱 看成体积
把 第$i$天买入第$i + 1$天卖出的利润 看成价值
可以无限次取

代码

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>

using namespace std;

const int N = 110, M = 10010;

int T, n, m;
int f[N]; //前i天max 
int g[M]; //第i天 背包 
int a[N][N];
int w[N][N];

int main()
{
	scanf("%d%d%d", &T, &n, &m);
	for (int i = 1; i <= T; i ++ )
		for (int j = 1; j <= n; j ++ )
			scanf("%d", &a[i][j]);	
	for (int i = 1; i <= T; i ++ )
		for (int j = 1; j <= n; j ++ )
			w[i][j] = a[i][j] - a[i - 1][j];
	
	f[1] = m;
	for (int i = 2; i <= T; i ++ )
	{
		for (int k = 0; k <= f[i - 1]; k ++ ) g[k] = 0;

		for (int j = 1; j <= n; j ++ )
			for (int k = a[i - 1][j]; k <= f[i - 1]; k ++ )
			{
				g[k] = max(g[k], g[k - a[i - 1][j]] + w[i][j]);
			}
		f[i] = g[f[i - 1]] + f[i - 1];
	}
	
	printf("%d\n", f[T]);
	
	return 0;
}