L
Description
称由 \(n\) 个点组成的无向图为简单的当且仅当满足如下条件：
- 对于任意两个不同的点 \((i,j)\) ，它们之间最多有 \(K\) 条简单路径。
如果某无向图为简单的，则记它的分数为
\[\prod_{1\le i<j\le n}A_{f_{i,j}}
\]
其中 \(n\) 为总点数，\(f_{i,j}\) 为 \(i,j\) 间的简单路径条数。
给定 \(M,K\)，对于 \(\forall n\in[2,M]\) 求出所有 \(n\) 个点的简单的无向图的分数之和对 \(998244353\) 取模的值。
\(M\le 10^5,0\le K\le3\)
Solution
\(K=0\)
不能连任何边，点数为 \(n\) 时答案为 \(A_0^{\binom{n}{2}}\)。
\(K=3\)
不存在两点之间有三条简单路径的情况下任意点对之间的简单路径条数不超过 \(3\)。
证明如下：
假设两点 \(1,3\) 间具有恰好 \(3\) 条简单路径，必有两条以上存在中转点，分这两条路径重合与不重合进行讨论：
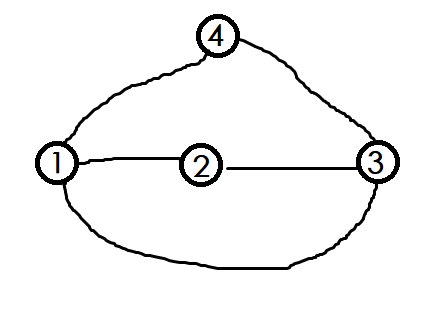
此情况 \(2,4\) 之间有 \(4\) 条简单路径。
此情况 \(1,4\) 之间有 \(4\) 条简单路径。
此情况 \(2,3\) 之间有 \(4\) 条简单路径。
综上所述，不存在无向图满足某两点间存在三条简单路径且所有点对间简单路径条数 \(\le 3\)。此情况同 \(K=2\)。
\(K=1\)
考虑 \(A_0=A_1=1\) 的情况，此时只需要进行不同图数目的计数。
此时的图是一个森林，\(n\) 个点时的答案记为 \(S_n\)，枚举森林中树的数目可得
\[S_n=\sum_{k=1}^{\infty}\frac{1}{k!}\sum_{\{m\}|\sum_{i=1}^km_i=n}1\times\prod_{i=1}^kf_{m_i}\times\binom{n-\sum_{j=1}^{i-1}m_i}{m_i}
\]
其中 \(f_i\) 代表 \(i\) 个节点的有标号无根树的数目，有矩阵树定理易得 \(f_1=1,f_i=i^{i-2}(i\ge2)\)
而
\[\prod_{i=1}^k\binom{n-\sum_{j=1}^{i-1}m_i}{m_i}=\frac{\prod_{i=1}^k\prod_{j=n-\sum_{j=1}^{i}m_i+1}^{n-\sum_{j=1}^{i-1}m_i}j}{\prod_{i=1}^km_i!}=\frac{n!}{\prod_{i=1}^km_i!}
\]
故上式可化为
\[S_n=\sum_{k=1}^{\infty}\frac{n!}{k!}\sum_{\{m\}|\sum_{i=1}^km_i=n}\prod_{i=1}^k\frac{f_{m_i}}{m_i!}
\]
考虑
\[\sum_{\{m\}|\sum_{i=1}^km_i=n}\prod_{i=1}^k\frac{f_{m_i}}{m_i!}
\]
观察到上式形如多项式乘法的形式，由于点有标号，故采用指数生成函数，记
\[Q(x)=\sum_{i=1}^\infty f_i\frac{x^i}{i!}
\]
则 \(Q(x)^k[x^n]\)，即多项式 \(Q(x)^k\) 中 \(\frac{x^n}{n!}\) 的系数为
\[\sum_{\{m\}|\sum_{i=1}^km_i=n}\frac{n!}{\prod_{i=1}^km_i!}\prod_{i=1}^
kf_{m_i}
\]
则
\[S_n=\sum_{k=1}^{\infty}\frac{Q(x)^k}{k!}=\exp(Q(x))
\]
写一个多项式exp即可。
考虑扩展情况，即 \(1\le A_i<998244353\)，此时
\[S_n=\sum_{k=1}^{\infty}\frac{1}{k!}\sum_{\{m\}|\sum_{i=1}^km_i=n}\prod_{i=1}^{k}v_{m_i}\times\prod_{i=1}^kf_{m_i}\times\binom{n-\sum_{j=1}^{i-1}m_i}{m_i}
\]
其中 \(v_i\) 代表大小为 \(i\) 的树产生的分数贡献，有
\[v_i=A_1^{\binom i2}\times A_0^{i(n-r)}
\]
其中 \(r\) 代表剩余点数。
于是
\[\prod_{i=1}^kv_{m_i}=\prod_{i=1}^{k}A_1^{\binom{m_i}2}A_0^{m_in-m_i\sum_{j=1}^{i-1}m_j}=A_0^{\frac{n^2}2}\prod_{i=1}^kA_1^{\binom{m_i}2}A_0^{-\frac{m_i^2}2}=A_0^{\binom n2}\prod_{i=1}^k(\frac{A_1}{A_0})^{\binom m2}
\]
令
\[Q(x)=\sum_{i=1}^\infty f_i(\frac{A_1}{A_0})^{\binom i2}\frac{x^i}{i!}
\]
则答案的生成函数即为 \(\exp(Q(x))\)，依次输出第 \(2\) 到 \(M\) 项即可。
\(K=2\)
先考虑 \(A_0=A_1=A_2=1\) 的弱化情况。
此时的图由多个连通块组成，每个连通块是基环树或者树。
对于大小为 \(i\) 基环树，记其内部的答案为 \(g_i\)，指数生成函数为 \(P(x)=\sum_{i=0}^\infty g_i\frac{x^i}{i!}\)，则最终答案的生成函数可表示为
\[S(x)=\exp(P(x)+Q(x))
\]
\(Q(x)\) 可以按照 \(K=1\) 时的方法来计算。
考虑基环树是一个大小为 \(m\) 的环加上 \(m\) 棵有根外向树（大小可为 \(1\)）所构成。
记有标号有根树的生成函数为
\[H(x)=\sum_{i=1}^\infty h_i\frac{x^i}{i!}
\]
其中 \(h_i=n^{n-1}\)，则
\[P(x)=\sum_{k=3}^\infty \frac{H(x)^k}{k!}\times \frac{(k-1)!}2=\sum_{k=3}^{\infty}\frac{H(x)^k}{2k}=\frac 12(-\ln(1-H(x))-H(x)-\frac{H(x)^2}2)
\]
计算出 \(P(x)\) 后可进一步得到答案的生成函数，扩展情况同 \(K=1\) 处理即可。
Code
点击查看代码
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <iostream>
#include <vector>
#include <cstring>
#define Mod 998244353
#define uint unsigned int
#define ll long long
using namespace std;
int Read() {
int x = 0; char ch = getchar();
while(!isdigit(ch)) ch = getchar();
while(isdigit(ch)) x = (x << 3) + (x << 1) + ch - '0', ch = getchar();
return x;
}
void Write(int x) {
if(x < 0) putchar('-'), x = -x;
if(x == 0) putchar('0');
int stk[55], tp = 0;
while(x) stk[++tp] = x % 10, x /= 10;
for(int i = tp; i; i--) putchar(stk[i] + '0');
}
int Add(int x, int y) {return (x + y >= Mod) ? x + y - Mod : x + y;}
int Dec(int x, int y) {return (x - y < 0) ? x - y + Mod : x - y;}
int mul(int x, int y) {return 1ll * x * y % Mod;}
uint qpow(uint a, int b) {uint res = 1; for(; b; b >>= 1, a = mul(a, a)) if(b & 1) res = mul(res, a); return res;}
namespace NTT {
int sz;
uint w[2500005], w_mf[2500005];
int mf(int x) {return (1ll * x << 32) / Mod;}
void init(int n) {
for(sz = 2; sz < n; sz <<= 1);
uint pr = qpow(3, (Mod - 1) / sz);
w[sz / 2] = 1; w_mf[sz / 2] = mf(1);
for(int i = 1; i < sz / 2; i++) w[sz / 2 + i] = mul(w[sz / 2 + i - 1], pr), w_mf[sz / 2 + i] = mf(w[sz / 2 + i]);
for(int i = sz / 2 - 1; i; i--) w[i] = w[i << 1], w_mf[i] = w_mf[i << 1];
}
void ntt(vector<uint>& A, int L) {
for(int d = L >> 1; d; d >>= 1)
for(int i = 0; i < L; i += (d << 1))
for(int j = 0; j < d; j++) {
uint x = A[i + j] + A[i + d + j];
if(x >= 2 * Mod) x -= 2 * Mod;
ll t = A[i + j] + 2 * Mod - A[i + d + j], q = t * w_mf[d + j] >> 32; int y = t * w[d + j] - q * Mod;
A[i + j] = x; A[i + d + j] = y;
}
for(int i = 0; i < L; i++) if(A[i] >= Mod) A[i] -= Mod;
}
void intt(vector<uint>& A, int L) {
for(int d = 1; d < L; d <<= 1)
for(int i = 0; i < L; i += (d << 1))
for(int j = 0; j < d; j++) {
uint x = A[i + j]; if(x >= 2 * Mod) x -= 2 * Mod;
ll t = A[i + d + j], q = t * w_mf[d + j] >> 32, y = t * w[d + j] - q * Mod;
A[i + j] = x + y; A[i + d + j] = x + 2 * Mod - y;
}
int k = (L & (-L));
reverse(A.begin() + 1, A.end());
for(int i = 0; i < L; i++) {
ll m = -A[i] & (L - 1);
A[i] = (A[i] + m * Mod) / k;
if(A[i] >= Mod) A[i] -= Mod;
}
}
}
struct poly {
vector<uint> a;
poly(int d = 0, int t = 0) {a.resize(d + 1); a[d] = t;}
uint& operator [] (const int& b) {return a[b];}
poly extend(int x) {poly c = *this; c.a.resize(x + 1); return c;}
int deg() {return a.size() - 1;}
void Print(int n) {for(int i = 0; i <= n; i++) Write(a[i]), putchar(' '); puts("");}
void resize(int x) {a.resize(x);}
int size() {return a.size();}
void Get(int n) {a.resize(n + 1); for(int i = 0; i <= n; i++) a[i] = Read();}
};
poly operator * (poly A, poly B) {
int n = A.deg() + B.deg() + 1, lim = 2;
for(; lim < n; lim <<= 1); NTT::init(lim);
A.resize(lim); B.resize(lim); NTT::ntt(A.a, lim); NTT::ntt(B.a, lim);
for(int i = 0; i < lim; i++) A[i] = mul(A[i], B[i]);
NTT::intt(A.a, lim); return A.extend(n - 1);
}
poly getinv(poly A) {
int n = A.size();
if(n == 1) return A[0] = qpow(A[0], Mod - 2), A;
poly B = A; B.resize((n + 1) >> 1); B = getinv(B);
int lim; for(lim = 2; lim < (n << 1); lim <<= 1); NTT::init(lim);
A.resize(lim); B.resize(lim); NTT::ntt(A.a, lim); NTT::ntt(B.a, lim);
for(int i = 0; i < lim; i++) A[i] = mul(Dec(2, mul(A[i], B[i])), B[i]);
NTT::intt(A.a, lim); return A.extend(n - 1);
}
poly getln(poly A) {
poly B; int n = A.size(); B.resize(n);
for(int i = 1; i < n; i++) B[i - 1] = mul(A[i], i); B[n - 1] = 0;
B = (B * getinv(A)).extend(n - 1);
poly C; C.resize(n);
for(int i = 1; i < n; i++) C[i] = mul(B[i - 1], qpow(i, Mod - 2)); C[0] = 0;
return C;
}
poly getexp(poly A) {
int n = A.size();
if(n == 1) return A[0] = 1, A;
poly B = A; B.resize((n + 1) >> 1); B = getexp(B).extend(n - 1);
poly C = getln(B);
for(int i = 0; i < n; i++) C[i] = Dec(A[i], C[i]); ++C[0];
return (B * C).extend(n - 1);
}
poly getmi(poly A, int k) {
int n = A.size(); poly B = getln(A);
for(int i = 0; i < n; i++) B[i] = mul(B[i], k);
return getexp(B);
}
int a[5], fac[100005] = {1}, finv[100005];
signed main() {
for(int i = 1; i <= 100000; i++) fac[i] = 1ll * fac[i - 1] * i % Mod;
int res = qpow(fac[100000], Mod - 2);
for(int i = 100000; i >= 0; i--)
finv[i] = res, res = 1ll * res * i % Mod;
int m = Read(), k = Read();
for(int i = 0; i <= k; i++) a[i] = Read();
if(k == 0) {
for(int n = 2; n <= m; n++)
printf("%lld ", 1ll * qpow(a[0], (1ll * n * (n - 1) / 2) % (Mod - 1)));
return 0;
}
if(k == 1) {
poly A; A.resize(m + 1);
A[0] = 0;
for(int i = 1; i <= m; i++)
A[i] = 1ll * (i == 1 ? 1 : qpow(i, i - 2)) * qpow(1ll * a[1] * qpow(a[0], Mod - 2) % Mod, (1ll * (i - 1) * i / 2) % (Mod - 1)) % Mod * finv[i] % Mod;
A = getexp(A);
for(int i = 1; i <= m; i++) A[i] = 1ll * A[i] * fac[i] % Mod;
for(int n = 2; n <= m; n++)
printf("%lld ", 1ll * qpow(a[0], (1ll * n * (n - 1) / 2) % (Mod - 1)) * A[n] % Mod);
return 0;
}
poly A; A.resize(m + 1);
A[0] = 0;
for(int i = 1; i <= m; i++)
A[i] = 1ll * qpow(i, i - 1) * qpow(1ll * a[1] * qpow(a[2], Mod - 2) % Mod, (1ll * i * (i - 1) / 2) % (Mod - 1)) % Mod * finv[i] % Mod;
poly C = A, D = A * A;
for(int i = 1; i <= m; i++)
C[i] = (Mod - A[i]) % Mod, D[i] = 1ll * D[i] * 499122177ll % Mod;
C[0] = 1;
poly B = getln(C);
for(int i = 1; i <= m; i++)
B[i] = (3ll * Mod - A[i] - D[i] - B[i]) % Mod * 499122177 % Mod * qpow(a[2], (1ll * i * (i - 1) / 2) % (Mod - 1)) % Mod * fac[i] % Mod;
for(int i = 1; i <= m; i++)
B[i] = (B[i] + 1ll * (i == 1 ? 1 : qpow(i, i - 2)) * qpow(a[1], (1ll * i * (i - 1) / 2) % (Mod - 1))) % Mod * qpow(qpow(a[0], (1ll * i * (i - 1) / 2) % (Mod - 1)) % Mod, Mod - 2) % Mod * finv[i] % Mod;
B = getexp(B);
for(int i = 1; i <= m; i++) B[i] = 1ll * B[i] * fac[i] % Mod;
for(int n = 2; n <= m; n++)
printf("%lld ", 1ll * qpow(a[0], (1ll * n * (n - 1) / 2) % (Mod - 1)) * B[n] % Mod);
return 0;
}