functions solution logic sets
VScode settings.json默认配置文件路径
Linux Ubuntu: > /home/${用户名}/.config/Code/User/settings.json Windows: > C:\Users\用户名\AppData\Roaming\Code\User 来源、参考: https://blog.csdn.net/cyqzy/arti ......
[CF1824D] LuoTianyi and the Function
## 题目描述 LuoTianyi gives you an array $ a $ of $ n $ integers and the index begins from $ 1 $ . Define $ g(i,j) $ as follows: - $ g(i,j) $ is the large ......
如何使用 ABAP Function Module SEO_CLASS_CREATE_COMPLETE 创建 ABAP class
`SEO_CLASS_CREATE_COMPLETE`函数模块用于在`SAP`系统中创建一个完整的`SAP`类。在`SAP ABAP`中,类是面向对象编程的基本构建块,它允许开发者将数据和行为组织到一个单一的实体中。`SAP`的类通常用于描述业务对象、数据结构和业务逻辑,以实现灵活性和可维护性。 ` ......
elasticsearch创建索引带mappings和settings
## 一、通过kabana控制台创建 我们在kabana控制台创建一个record_feature_tag的索引,对应的mapping配置如下 ```js PUT /record_feature_tag { "mappings": { "properties" : { "_class" : { "t ......
Custom ASAN_OPTIONS set without abort_on_error=1
background: when i want to run AFL . I met this issue. and either set export ASAN_OPTIONS=abort_on_error=0 nor export ASAN_OPTIONS=abort_on_error=1 do ......
MAUI 本地数据sqlite 报错 : Cannot update Settings: it has no PK
原因是没有设置主键,需要标记主键 [PrimaryKey] public class Settings { [PrimaryKey] public string Key { get; set; } public string Value { get; set; } } ......
unordered_set 的初始化方法
unordered_set是一个哈希表的实现,因此初始化其实就是给它分配一定的空间,并且指定哈希表中每个元素的存储方式。 unordered_set的初始化方式有以下几种: 无参构造函数 std::unordered_set<int> mySet; 默认情况下,unordered_set会分配一定的 ......
本地nacos启动报错: Please set the JAVA_HOME variable in your environment, We need java(x64)! jdk8 or later is better!
编辑startup.cmd文件 将模式从cluster改为standalone 插入一行指定你的JAVA_HOME路径set JAVA_HOME="C:\dev_files\jdk17" 然后启动nacos即可~ ......
【Azure Function App】Nodejs Function遇见WorkerProcessExitException : node exited with code -1073740791 (0xC0000409) 错误
Exception while executing function: Functions.AzureBlobTrigger ---> Microsoft.Azure.WebJobs.Script.Workers.WorkerProcessExitException : node exited wi... ......
this.$set的使用方法
//对象的属性sex的值更新为"男" let obj = {name:"六四",age:18,sex:"女"} this.$set(obj,"sex","男") //第一个参数是对象,第二个参数是更新的属性名称,第三个参数是新的内容 //更新之后的obj是 {name:"六四",age:18,sex ......
[React Typescript] Function overload in React hook
import { useState } from "react"; import { Equal, Expect } from "../helpers/type-utils"; type UseStateReturnValue<T> = { value: T; set: React.Dispatch ......
Set Theory: Cardinality + Infinity comparation
Infinity Counting + Comparation: https://brilliant.org/courses/infinity/introduction-87/how-to-count-to-infinity/ Cardinality VS Tagging: Review and R ......
Callback Function Essence
# Include Example 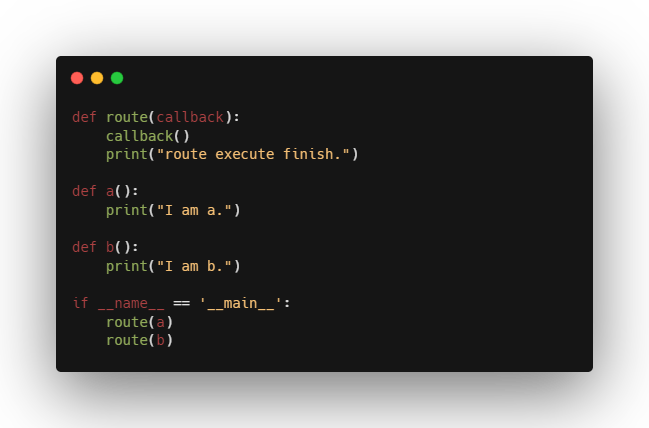 Input: ``` I am a. route execute finis ......
python+playwright 学习-74 set_extra_http_headers设置浏览器请求头部
# 前言 大部分网站保存登录状态是用cookies,也有个别网站是在请求头部添加token实现保存登录。 playwright 可以使用set_extra_http_headers() 方法设置浏览器请求头部参数 # set_extra_http_headers() 方法 设置头部参数headers ......
Spring set 注入不同类型的参数
### **案例** - 建立复杂的数据类型 Student类 ```java public class Student { private String name; private Address address; private List books; private Map card; pri ......
KubeSphere 社区双周报 | Java functions framework 支持 SkyWalking | 2023.8.4-8.17
KubeSphere 社区双周报主要整理展示新增的贡献者名单和证书、新增的讲师证书以及两周内提交过 commit 的贡献者,并对近期重要的 PR 进行解析,同时还包含了线上/线下活动和布道推广等一系列社区动态。 本次双周报涵盖时间为:2023.08.04-2023.08.17。 ## 贡献者名单 ! ......
20230818 CHAPTER 6 Functions and the Stack 函数和栈
x31 arm SP寄存器 16byte对齐 调用函数,必须保存当前位置以便函数调用完成后返回,the link register (LR) which is X30, branch with link (BL) bl 与b 类似,不同的是 bl 在跳转前把下一条指令的地址保存在LR寄存器中,这样b ......
vue3传属性时报错 [Vue warn]: Component is missing template or render function.
上网查这个问题,解决方案很多,没有一款适合我。。。先说我的解决办法,如果解决不了再往下看,我的原因是 用的子组件的ref和子组件的标签名一样了: <ChildComponent1 ref="ChildComponent1" :parent-data="data" > <template #slot- ......
【校招VIP】java语言类和对象之map、set集合
考点介绍:map、set集合相关内容是校招面试的高频考点之一。 map和set是一种专门用来进行搜索的容器或者数据结构,其搜索效率与其具体的实例化子类有关系。 一、考点题目1、HashMap 为什么线程不安全? 解答:并发赋值被覆盖: 在 createEntry 方法中,新添加的元素直接放在头部,使 ......
哈希表(实现 Python 中的集合 set)
> 博客地址:https://www.cnblogs.com/zylyehuo/ ```python # -*- coding: utf-8 -*- class LinkList: class Node: def __init__(self, item=None): self.item = item ......
关于 SAP ABAP Enqueue Function Module 的输入参数 _wait
我们查看 ABAP 系统根据 Lock Object 自动生成的 Enqueue Function Module,可以发现它有一个名叫 `_wait` 的输入参数,默认值为 `space`: 之一:Flink基于set实时uv统计
UVStatMultiPlans(GitHub)项目持续收集各种高性能实时uv实现方案并对各种实现方案的优缺点进行对比分析! #### 需求描述 统计每分钟用户每个页面的uv访问量。 #### Kafka数据格式 ``` {"userId":"c61b801e-22e7-4238-8f67-9096 ......
Set A Light 3D Studio Mac三维模拟影棚布光软件
SetA Light3D Studio是一款全新的专业三维模拟影棚灯光布光软件,支持在 Mac平台上制作虚拟摄影棚,能够快速制作出真实影棚布光效果,可以使用专业的灯光器材和道具。软件功能强大,操作简单,是一款功能强大的专业三维模拟影棚灯光软件。 SetA Light3D Studio Mac版是一个 ......
teamcenter 报错:Could not open FcCJavaclientProxy library. Make sure FMS_HOME is set properly
报错: 解决方法: 路径相应改一下 ......
什么是 SAP ABAP 系统的 LUW (Logical Unit of Work)概念
在SAP ABAP系统中,数据库LUW是一个关键概念,用于管理数据库操作的一致性和隔离性。 `数据库LUW(Logical Unit of Work)的概念`: 在SAP ABAP系统中,数据库LUW是一组数据库操作的逻辑集合,这些操作要么全部成功地提交到数据库,要么全部回滚。它确保了数据库操作的一 ......
[Typescript] Don't compare generic function, instead compare function arguments and return type
Typescript has its problem that when you try to compare generic function to a function signature, you will run into issue. Because for one function, i ......